This post assumes you have read the first, which introduces generalized polynomial counting, and the second, which restricts the focus and specifies the general aim.
Gray Silver
As previously shown, the golden ratio (recurrence \langle 1, 1|) can be generalized in several ways. The silver ratio was introduced as the next “metallic mean”, a sequence of quadratic roots of the form \langle n, 1|, and the limiting ratios of the corresponding recurrences. These roots have a (simple) continued fraction expansion:
\begin{gather*}
\langle n, 1| ~~\iff~~ x^2 - nx - 1 \\
x^2 = nx + 1 ~~\implies~~
x = n + \frac{1}{x} \\
x = n + \cfrac{1}{n + \cfrac{1}{n + \cfrac{1}{n + \cfrac{1}{\ddots}}}} = [n; \underline{n}]
\end{gather*}Again, the underline denotes repetition, since the overbar has been used for negation. When we examined the Jacobsthal base, we tried flipping n and 1 before seeing that the system was hard to manipulate. However, parametrizing in both terms (recurrence \langle n, n|) demonstrates a strange duality with the above continued fraction:
\begin{gather*}
\langle n, n| ~~\Leftrightarrow~~ x^2 - nx - n \\
x^2 = nx + n ~~\Rightarrow~~
x = n + \frac{n}{x} \\
x = n + \cfrac{n}{n + \cfrac{n}{n + \cfrac{n}{n + \cfrac{n}{\ddots}}}} =
n + \cfrac{\textcolor{red}{\cancel{n}}}{\textcolor{red}{\cancel{n}} + \cfrac{\textcolor{red}{\cancel{n}}}
{n + \cfrac{\textcolor{blue}{\cancel{n}}}{\textcolor{blue}{\cancel{n}} + \cfrac{\textcolor{blue}{\cancel{n}}}{\ddots}}}} \\
x = n + \cfrac{1}{1 + \cfrac{1}{n + \cfrac{1}{1 + \cfrac{1}{\ddots}}}} =
[n; \underline{1, n}]
\end{gather*}In other words, the root of \langle n, 1| has continued fraction n repeating, and the root of \langle n, n| has continued fraction n, 1 repeating.
After the golden ratio, the next term in in the latter series is the recurrence \langle 2,2. It produces the series 0, 1, 2, 6, 16... (OEIS A002605), and the limiting ratio of its successive terms is 1 + \sqrt 3 \approx 2.7321.... This value and the polynomial coefficients are bounded above by 3, so it stands to reason that a ternary alphabet is suitable. The trick for expanding 3 works as before:
\textcolor{red}{3}00 = 2\textcolor{red}{22}
= \textcolor{blue}{22}2 = \textcolor{blue}{1}002 Unnamed Unnamed
Ratio Sequence
____
210 1234 6 2 1
0 0 0
1 1 1
2 2 1 0
3 10.02 1 1
4 11.02 2 0
5 12.02 2 1
6 20.1102 1 0 0
7 21.1102 1 0 1
8 100.1102 1 1 0
9 101.1102 1 1 1
10 102.1102 1 2 0In an homage to heraldry terminology, I choose to call this system cendrée, and the root of the polynomial the ashen ratio (abbreviated \kappa). Gold and silver (“or” and “argent”) are “metals”; cendrée is a non-standard color referring to an ashen gray, which reflects its relationship to the metallic means.
Ash on the Fulcrum
Each fractional expansion in the table above appears to end in “2”. I’ve actually checked this for the first 1000 integers and found no expansions which do not terminate in “2” besides 0 and 1. In contrast, the silver ratio expansions end in both 1 and 2. While it isn’t a problem with the fractional base on its own, things get complicated when considering a balanced alphabet.
\begin{gather*}
\textcolor{red}{2.0} =
\textcolor{red}{1}0.\textcolor{blue}{\bar{2}0} =
1\textcolor{blue}{\bar{1}}.0\textcolor{orange}{20} =
1\bar{1}.\textcolor{orange}{1}0\bar{2} = ... =
1\bar{1}.\underline{1\bar{1}}\\
\textcolor{green}{2} =
1\bar{1}.0\textcolor{green}{2} =
1\bar{1}.1\bar{1}0\textcolor{green}{2} = ... =
1\bar{1}.\underline{1\bar{1}}\\
\end{gather*}The number 2 happens to have an repeating balanced expansion. The first approach is the iterative application of the carry, while the second notices the recursion induced by the symbol “2”. Both of these derivations involve an infinite number of steps, so there might still be a nagging suspicion that this is invalid. In fact, the we can derive the carry polynomial directly from this series (and vice versa) using a geometric series argument:
\begin{gather*}
1.\underline{\vphantom{\bar{1}}1}_x
= 1 + x^{-1} + x^{-2} + x^{-3} + x^{-4} + ...
= \frac{1}{1 - (1/x)} = \frac{x}{x - 1} \\
1.\underline{\bar{1}1}_x
= 1 -\ x^{-1} + x^{-2} -\ x^{-3} + x^{-4} - ...
= \frac{-x}{-x -\ 1}
= \frac{x}{x + 1} \\
2 = 1\bar{1}.\underline{1\bar{1}}_x
= \frac{x^2}{x + 1} \\
x^2 = 2x + 2
\end{gather*}We assume both series converge, since \kappa > 1. Repeating expansions in integral bases are typically strange-looking expressions like 0.\underline{9} = 1, and their only use is for rational numbers. For example, we can evaluate this expression [kappa]\frac{x^2}{x + 1}[/kappa] at x = 3 to interpret “1.\underline{\bar{1}1}” as a ternary (base 3) expansion. I happens to be the rational value 9/4 = 2.25_{10}. But the irrational base \kappa breaks that rule, and a repeating expansion is necessary to represent an integer.
Mixing Ashes
In the balanced silver ratio base, we had the choice of forbidding either of “11” or “10“. This was because when the carry was applied to either string, the negative of the other would appear. In this system, the dilemma is instead whether to forbid “11” or its negative, since carrying at one produces the other. I choose to permit positive adjacent 1’s since both terms of the carry are positive.
I suspect that the only repeating string which occurs in the integers is 0.\underline{1\bar{1}} and shifts thereof, but have no proof. If we use the digit “2” to represent the repeating string, we can write mixed balanced expansions of integers. However, we must remember to forbid “102”, since it would expand to “11\bar{1}.\underline{1\bar{1}}“, which has two adjacent 1’s.
Mixed Cendree Balanced Cendree
______ ____|__
3210 123456 3210 1234|56 (repeating)
0 0 0
1 1 1
2 2 1T.1T1T 1T...
2 1T.02 1T.1T1T 1T...
3 10.02 10.1T1T 1T...
4 1TT.02 1TT.1T1T 1T...
5 1T0.02 1T0.1T1T 1T...
6 10T.TT02 10T.TT1T 1T...
7 100.TT02 100.TT1T 1T...
8 101.TT02 101.TT1T 1T...
9 101.1102 101.111T 1T...
9 1TTT.0TTT02 1TTT.0TTT 1T...
10 1TT0.0TTT02 1TT0.0TTT 1T...Note that at the transition from 8 to 9, instead of incrementing the 1, the string “0.\bar{1}\bar{1}” was incremented to “0.11“. Similar strategies must be used for larger numbers.
Flip it Radix-ways
Repeating expansions usually come from fractions whose denominator is coprime to the base. It is possible to convert such numbers into the ratio of two integers by using a fairly simple procedure. Here it is applied to both 0.\underline{69}_{10} and the string in question, “0.1\bar{1}“:
\begin{gather*}
{0.\underbrace{
\underline{\textcolor{blue}{69}}_{10}
}_{\text{length } \textcolor{red}{2}}}
= \frac{\textcolor{blue}{69}_{10}}{10^{\textcolor{red}{2}} - 1}
= \frac{\textcolor{blue}{69}_{10}}{99_{10}}
= \frac{23_{10}}{33_{10}}
\\
0.\underline{
\textcolor{blue}{1\bar{1}}}_p
= \frac{\textcolor{blue}{1\bar{1}}_p}{p^2 - 1}
= \frac{p - 1}{p^2 - 1}
= \frac{1}{p + 1}
\end{gather*}These fractions can be used to construct p–adic numbers. For our purpose, this essentially places a p^n - 1 in the numerator and asserts that that p^\infty \rightarrow 0. For a length-2 repeating expansion, n is even, and the following quotients produce truncations:
\begin{align*}
&\frac{p^2 - 1}{p+1} = \frac{10\bar{1}}{11}
& \substack{
\phantom{11}{\underline{\phantom{)1}
1\bar{1}}} \\
11)10\bar{1} \\
\phantom{11)}\underline{11} \phantom{0} \\
\phantom{11)1}{\bar{1}\bar{1}} \\
\phantom{11)1}{\underline{\bar{1}\bar{1}}} \\
\phantom{11)1}00
} \\ \\
&\frac{p^4 - 1}{p+1} = \frac{1000\bar{1}}{11}
& \substack{
\phantom{11}{\underline{\phantom{)1}
1\bar{1}1\bar{1}}} \\
11)1000\bar{1} \\
\phantom{11)} \underline{11} \phantom{000} \\
\phantom{11)1} \bar{1}0 \phantom{00}\\
\phantom{11)1} \underline{\bar{1}\bar{1}} \phantom{00} \\
\phantom{11)10}10 \phantom{0} \\
\phantom{11)10} \underline{11} \phantom{0} \\
\phantom{11)100} \bar{1}\bar{1} \\
\phantom{11)100} \underline{\bar{1}\bar{1}} \\
\phantom{11)100} 00 \\
}
\end{align*}In the limit, the quotient is “…1\bar{1}1\bar{1}1\bar{1}“, which is actually the negative of {1 \over p+1} due to the negative sign in the numerator. Since we’re using a balanced alphabet, negation is simply replacing “\bar{1}” with “1” and vice versa, producing…
0.1\bar{1}1\bar{1}1\bar{1}..._\kappa = ...\bar{1}1\bar{1}1\bar{1}1\bar{1}1_\kappa \\
0.\underline{1\bar{1}}_\kappa = \underline{\bar{1}1}\bar{1}1_\kappa…which is the initial expansion, but flipped about the radix point. The final balanced \kappa-adic expansion for 2 can then be acquired through simple addition:
\begin{align*}
&\phantom{+} 1\bar{1}.000000..._\kappa
~=~ ...000001\bar{1}_\kappa \\
&+ \underline{00.1\bar{1}1\bar{1}1\bar{1}..._\kappa
~=~ ...1\bar{1}1\bar{1}1\bar{1}1}_\kappa \\
& \phantom{+} 1\bar{1}.1\bar{1}1\bar{1}1\bar{1}..._\kappa
~=~ ...1\bar{1}1\bar{1}100_\kappa \\
\end{align*}Reading these expansions as power series, we can convert them into a rational expression
\begin{align*}
2 = ...1\bar{1}1\bar{1}100_\kappa
&=\kappa^2 - \kappa^3 + \kappa^4 - \kappa^5 +... \\
&= \kappa^2(1 - \kappa + \kappa^2 - \kappa^3 +...) \\
&= \kappa^2 \cdot \frac{1}{1 - (-\kappa)} \\
&= \frac{\kappa^2}{\kappa + 1}
\end{align*}This is the same as the previous expression for 2. In a roundabout way, by borrowing p-adic ideas, we showed another way this is true by using power series manipulations. This also means that the long division above is in fact polynomial long division.
Two Plus Two Equals Chaos
p-adic expansions are still expressions in the base p, so the carry rule still applies. However, since the carry continues to infinity, we must at some point truncate the expansions to keep them within view. When p is an integer, the carry is a single digit wide, and we can demarcate a repeating section.
\kappa is not an integer, and its carry has length 2. While the \kappa-adic expansion for 2 can be incremented once to produce a valid one one for 3, problems arise when attempting to construct 4. The most direct method is to start with the symbol “4” and manipulate it:
4 = 2\bar{4}0
= \bar{2}600
= 3\bar{8}000
= \bar{4}\text{B}0000
= 5\bar{\text E}10000
= \text{J}0\textcolor{red}{1}0000
= ...(Latin characters used as digits start at A for ten, as in hexadecimal.) Even though the most significant digit grows larger, a residual “1” (marked in red) is left behind. We can produce more terms indefinitely, but as shown, the “head digit” where the carry takes place starts to grow.
Alternative Constructions
To keep the head small, it would be nice if it were taken mod an integer. Both \bar{1} and 1 are odd, so one might hope that in between carries, mod 2 can be applied somewhere. Unfortunately, this is not the case. To produce the “3” seen in “3\bar{8}000“, “6” must be carried appropriately. To capture this difference, we must upgrade the modulus to 8 (as 7 would ruin the parity). But this means that the expansion of 4 is “30000“, so 8 must also be upgraded. Such upgrades occur ad infinitum, since the carry applies across all higher place values.
Instead of expanding “4” directly, we have other options available.
- Add the nonrepeating part of the mixed balanced expansion of 4 with the \kappa-adic version of the repeating part (Another direct manipulation)
- Increment the least significant digit in the expansion of 2 twice (Addition)
4 = 2 + 2 = \frac{x^2}{1 + x} + 2 = ...\bar{1}1\bar{1}102_x- Add the expansion of 2 to itself (Multiplication)
4 = 2 \cdot 2 = \frac{2x^2}{1 + x} = ...\bar{2}2\bar{2}200_x- Square the power series expansion of 2 (Exponentiation)
\begin{gather*}
4 = 2^2 = \left(\frac{x^2}{1 + x}\right)^2 =
-x^4 \left(\frac{d}{dx}\frac{1}{1 + x}\right) = ...\bar{4}3\bar{2}10000_x
\end{gather*}If all of these series are expansions of 4, then they should produce the same string after applying the carry enough times. Fortunately, this seems to be the case, as this table demonstrates:
\begin{array}{}
{x^2 \over 1 + x} + 2 &\phantom{00}&
{2x^2 \over 1 + x} &\phantom{00}&
\left({x^2 \over 1 + x}\right)^2 \\[10pt] \hline
\vphantom{2^{2^{2^2}}}...\bar{1}1\bar{1}1\bar{1}102 \\[4pt]
...\bar{1}1\bar{1}1\bar{1}2\bar{2}0 \\[4pt]
...\bar{1}1\bar{1}1\bar{2}400 &&
...\bar{2}2\bar{2}2\bar{2}200 \\[4pt]
...\bar{1}1\bar{1}3\bar{6}000 &&
...\bar{2}2\bar{2}3\bar{4}000 \\[4pt]
...\bar{1}1\bar{4}90000 &&
...\bar{2}2\bar{4}70000 \\[4pt]
...\bar{1}5\bar{\text C}10000 &&
...\bar{1}5\bar{\text A}10000 &&
...\bar{4}3\bar{2}10000 \\[4pt]
...\bar{7}{\text H}010000 &&
...\bar{6}\text F010000 &&
...\bar{5}5010000 \\[4pt]
...\bar{\text N}1010000 &&
...\bar{\text L}1010000 &&
...\bar{9}1010000 \\[4pt]
\textcolor{green}{...\bar{1}1010000} &&
\textcolor{green}{...\bar{1}1010000} &&
\textcolor{green}{...\bar{1}1010000}
\end{array}The rightmost series is the most resilient to the carry head growth, but this comes at the cost of not operating on a repeating series. In the range shown, all three columns converge to the same digit sequence, which truncated to 20 terms is:
4 = …\bar{1}00000\bar{1}00001\bar{1}1010000_\kappa = \kappa^4 + \kappa^6 -\ \kappa^7 + ...Contrary to the sequence used to build it, this expansion appears to be nonrepeating. As of writing, there are no matches in the OEIS, even if the leading 0’s are ignored. The Haskell used to generate each expansion above can be found here, and the first 8192 digits be found in a CSV here.
All Positive
If we are slightly greedier with the carry, we can clear it of all negative digits. The initial terms are the same, but diverge after the first \bar{1} which appears in the sequence.
4 = ...1100000011111010000_\kappa = \kappa^4 + \kappa^6 + \kappa^7 + \kappa^8 + ...
Again, it appears to be possible to achieve this sequence by applying the carry enough times, starting with any of the alternative expansions. A similar CSV containing 8192 terms is available here.
This alternate expansion is somewhat confounding, since \kappa is bounded above by the integer 3 and should therefore require three symbols in its alphabet. I can think of two explanations, and do not know whether either of them are correct:
- The expansion is related to the conjugate root \kappa^* = 1 -\ \sqrt 3 \approx -0.73205.... The reciprocal of this number is less than two.
- Because infinite precision is required, the minimal alphabet can become (possibly arbitrarily) small.
Four-ier Transforms
The discrete Fourier transform is an operation on regular samples of a function, or more generally, numeric sequences. It converts highly repetitive sequences to sequences with peaks. Since we’re dealing with infinite expansions, we’ll need to truncate at some point. If the period is very large, so must be the truncation.
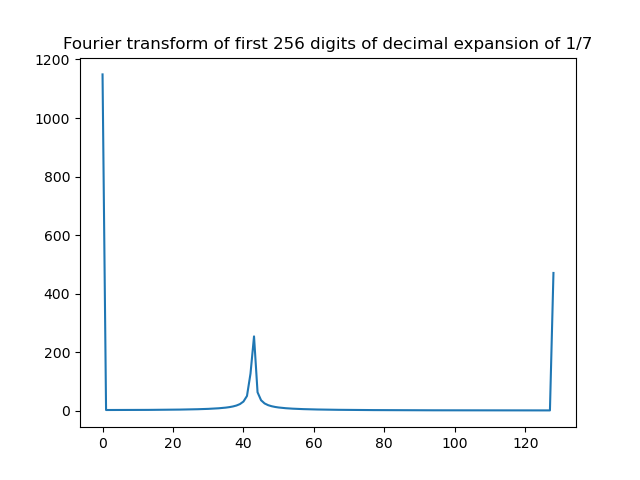
For example, the digits in the decimal expansion of 1/7 form the string “1, 4, 2, 8, 5, 7”, repeating. The graph below is the plot of the DFT of the first 256 terms of the sequence. The clear peak between terms 42 and 43 is because the expansion repeats every 6 terms and {256 \over 43} < 6 < {256 \over 42}.
If the \kappa-adic expansion of 4 is nonrepeating, then its DFT should not have any noticeable peaks. The DFT of the first 256 terms shows it to be very noisy.
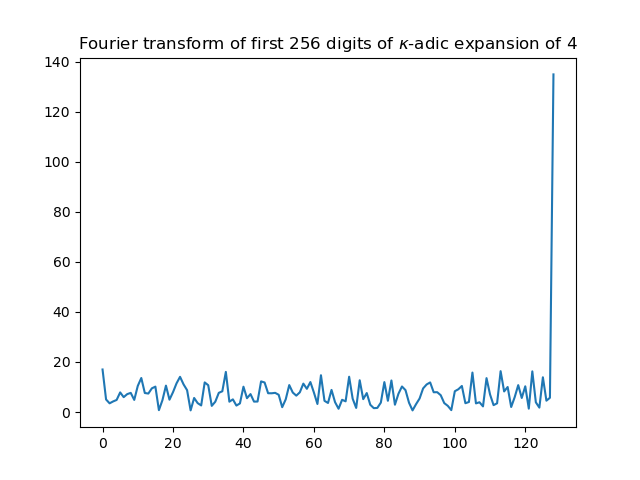
There is a pronounced spike at the right edge of the graph (the Nyquist frequency), but it has a simple explanation: “1” appears only at even place values and “\bar{1}” at odd. At Nyquist, the DFT degenerates into an alternating sum, so its value is simply the number of nonzero digits. If we map the negatives out of the sequence, the peak is destroyed.
Even in the 8192-term truncation, there are no noticeable spikes in its DFT, lending further credence to its aperiodicity. Though I will not show it here, the same applies to the binary sequence shown previously.
Much like the expansion of irrational numbers in integral bases, the balanced \kappa-adic expansion of 4 is(?) nonrepeating. This is surprising, especially since 4 has a terminating expansion in a non-balanced alphabet and a repeating expansion in a balanced one.
Closing
This concludes the discussion of \kappa-adic numbers. The next post will return to integral sequences, and the patterns produced from their “erroneousness” as an actual base.
Update: I am unsure whether \kappa‘s proximity to e produces some of these effects, or if it is somehow more ideal than other roots whose repeating fraction expansion is [n; \underline{1, n}] (for integral n). It is easy to see that repeating expressions like n = 10.\bar{n} = 1\bar{1}.\underline{1\bar{1}} will occur in each of these, but \kappa still bears the distinction of needing only 0.1\bar{1} as a repeating element for integers.
Base e, while it lacks an explicit carry, has the lowest radix economy, meaning it takes the fewest digits to express a number with respect to the size of its minimal alphabet. I would be interested to know if other monic polynomials whose root is approximately e share some of \kappa‘s strange properties.